Solución de Ecuaciones Cuadráticas por Factorización
Objetivo de Aprendizaje
· Resolver ecuaciones cuadráticas usando técnicas de factorización y expresar la solución como un conjunto.
Introducción
Cuando un polinomio es igual a cierto valor (ya sea un entero u otro polinomio), el resultado es una ecuación. Una ecuación que puede ser escrita de la forma ax2 + bx + c = 0 se llamaecuación cuadrática. Podemos resolver estas ecuaciones cuadráticas usando las reglas del álgebra, aplicando técnicas de factorización donde sea necesario, y usando la Propiedad Cero de la Multiplicación.
La Propiedad Cero de la Multiplicación establece (¡en términos algebraicos, por supuesto): si el producto de dos números es 0, entonces por lo menos uno de los factores es 0.
Propiedad Cero de la Multiplicación
Si ab = 0, entonces ya sea a = 0 o b = 0, o ambos a y b son 0.
|
Esta propiedad puede parecer obvia, pero tiene importante implicaciones en cómo resolvemos ecuaciones cuadráticas: significa que si tenemos un polinomio factorizado igual a 0, podemos estar seguros de que al menos uno de sus factores es también 0. Podemos usar este método para identificar soluciones de una ecuación.
Pero nos estamos adelantando — empecemos con un ejemplo de una ecuación cuadrática y pensemos en cómo resolverla. La ecuación 5a2 + 15a = 0 es una ecuación cuadrática porque puede escribirse como 5a2 + 15a + 0 = 0, que es equivalente a la forma ax2 + bx + c = 0, con c = 0.
Ejemplo
| |||
Problema
|
Resolver a en 5a2 + 15a = 0
| ||
5a2 + 15a = 0
|
El problema nos pide resolver a; empecemos por factorizar el lado izquierdo de la ecuación
| ||
5(a2 + 3a) = 0
|
5 es factor común de 5a2 y 15a.
| ||
5a(a + 3) = 0
|
a es factor común un de a2 y 3a.
| ||
En este punto hemos factorizado completamente el lado izquierdo de la ecuación. Si sólo quisiéramos factorizar la expresión, podríamos parar aquí, pero recuerda que estamos resolviendo a de la ecuación.
Aquí es donde usamos la Propiedad Cero de la Multiplicación. Ya que toda la expresión es igual a cero, sabemos que por lo menos uno de los términos, 5a o (a + 3), tiene que ser igual a cero. Vamos a continuar con la solución de este problema igualando cada término a cero y resolviendo las ecuaciones.
5a = 0 a + 3 = 0
|
Igualar cada factor a cero
| ||
a = 0 a = -3
|
Resolver la ecuación
| ||
Solución
|
a = 0 o a = -3
|
Resultan dos valores posibles de a: 0 y -3. (Estos valores también se llaman raíces de la ecuación.) Para comprobar nuestras respuestas, podemos sustituir ambos valores directamente en nuestra ecuación original y ver si obtenemos una expresión válida para cada una.
Comprobando a = 0
|
Comprobando a = -3
|
5a2 + 15a = 0
|
5a2 + 15a = 0
|
5(0)2 + 15(0) = 0
|
5(-3)2 + 15(-3) = 0
|
5(0) + 0 = 0
|
5(9) – 45 = 0
|
0 + 0 = 0
|
45 – 45 = 0
|
0 = 0
|
0 = 0
|
Sustituir estos valores en la ecuación original produce dos expresiones correctas, entonces sabemos que nuestros valores son correctos. Esta ecuación cuadrática, 5a2 + 15a = 0, tiene dos raíces: 0 y -3.
Podemos usar el Producto Cero de la Multiplicación para resolver ecuaciones cuadráticas de la forma ax2 + bx + c = 0. Primero factorizamos la expresión, y luego resolvemos cada una de las raíces.
Ejemplo
| ||||
Problema
|
Resolver r.
r2 – 5r + 6 = 0.
| |||
r2 – 3r – 2r + 6 = 0
|
Expandir el término -5r usando dos coeficientes tales que su suma sea -5 y su producto sea 6.
| |||
(r2 – 3r) – (2r – 6) = 0
|
Agrupar términos
| |||
r(r – 3) – 2(r – 3) = 0
|
Sacar los factores comunes de cada grupo
| |||
(r – 3)(r – 2) = 0
|
Usar la Propiedad Distributiva para sacar (r – 3) como un factor
| |||
r – 3 = 0
|
r – 2 = 0
|
Usar la Propiedad Cero de la Multiplicación para igualar cada factor a 0
| ||
r = 3
|
r = 2
|
Resolver la ecuación
| ||
Solución
|
r = 3 o r = 2
|
Las raíces de la ecuación original son 3 o 2
| ||
La solución de esta ecuación es r = 2 o r = 3, ya que ambos valores de r resultarán en una expresión válida. (¿Escéptico? Sustituye r por los valores 2 y 3 en la ecuación original. Te esperamos.)
Resolver h:
h(2h + 5) = 0
A) h = 0
B) h = 2 o 5
C) h = 0 o 2.5
D) h = 0 o -2.5
|
Aplicando la Propiedad Cero de la Multiplicación
Cuando usamos la Propiedad Cero de la Multiplicación para resolver una ecuación cuadrática, necesitamos asegurarnos que la ecuación este igualada a cero. Algunas veces esto requerirá de mover los términos para que quede 0 en un lado de la ecuación.
Como un ejemplo, piensa en la ecuación 12x2 + 11x + 2 = 7. Podríamos factorizar el trinomio del lado izquierdo de la ecuación tal como esta, pero nos quedaría la ecuación (4x + 1)(3x + 2) = 7. ¡Y es hasta aquí a donde podemos llegar! Esta nueva ecuación nos dice que los dos factores, (4x + 1) y (3x + 2), son iguales a 7 cuando son multiplicados. Igualar cada factor a 7 y luego resolver la ecuación tampoco nos ayuda; no estamos buscando los factores que son 7; sino los factores que, cuando se multiplican, son iguales a 7. Es decir, ¡no podemos usar la Propiedad Cero de la Multiplicación cuando no hay un cero en el otro lado de la ecuación!
¿Entonces cuál es la solución? Para tener un cero en un lado de la ecuación, debemos restar 7 de ambos lados. Esto significa que nuestra ecuación cuadrática de 12x2 + 11x + 2 = 7 se convierte 12x2 + 11x – 5 = 0. Podemos factorizar el trinomio en lado izquierdo y luego usar la Propiedad Cero de la Multiplicación para encontrar los valores de x.
El ejemplo siguiente muestra cómo resolver una ecuación cuadrática donde ningún lado es originalmente igual a cero. (Nota que la secuencia de factorización ha sido acortada.)
Ejemplo
| ||||
Problema
|
Resolver b en 5b2 + 4 = -12b
| |||
5b2 + 4 + 12b = -12b + 12b
|
La ecuación original tiene
-12b a la derecha. Para hacer este lado igual a cero, sumar 12b a ambos lados
| |||
5b2 + 12b + 4 = 0
|
Combinar términos semejantes
| |||
5b2 + 10b + 2b + 4 = 0
|
Reescribir 12b para agrupar y factorizar fácilmente
| |||
5b(b + 2) + 2(b + 2) = 0
|
Usar la Propiedad Distributiva para sacar los factores comunes de los pares de términos
| |||
(5b + 2)(b + 2) = 0
|
Usar la Propiedad Distributiva para sacar el factor (b + 2). La cuadrática queda completamente factorizada
| |||
5b + 2 = 0
|
b + 2 = 0
b = -2
|
Aplicar la Propiedad Cero de la Multiplicación
| ||
Solución
| ||||
Algunas veces podemos factorizar ecuaciones cuadráticas que resultan así: 8(x + 3)(x + 2) = 0. Sabemos cómo aplicar la Propiedad Cero de la Multiplicación a los factores (x + 3) y (x + 2), pero ¿qué hacemos con el coeficiente 8? ¿Podemos aplicar la Propiedad Cero de la Multiplicación a un entero?
En esta situación tenemos 3 factores: 8, x + 3, y x + 2. La regla de la Propiedad Cero de la Multiplicación nos dice que si el producto de tres factores, 8(x + 3)(x + 2), va a ser igual a cero en el lado derecho de la ecuación, la única manera de que eso pueda pasar es si por lo menos uno de los tres factores en el lado izquierdo es 0. Entonces probemos cada uno de ellos:
El factor 8 nunca será igual a 0, entonces podemos simplemente ignorarlo como una de las posibilidades.
El factor x + 3 podría ser igual a cero, y lo es cuando x = -3 entonces lo es.
El factor x + 2 podría ser igual a cero, y lo es cuando x = -2 entonces lo es.
Entonces nuestras soluciones para la ecuación original son x = -3 o x = -2, el factor 8 no contribuye a una tercera solución.
Resolver m.
2m2 + 10m = 48
A) m = 3 o -8
B) m = -3 o 8
C) m = 0 o -5
D) m = 0 o 5
|
Ejemplos:
1) Resuelva ( )( ) x +3 2x −1 = 9 .
Solución:
Lo primero es lograr que la ecuación se iguale a cero. Para esto, primero
multiplicaremos el lado izquierdo y luego restaremos el nueve. Después
factorizaremos la ecuación resultante para obtener la solución final. Es
conveniente verificar la solución final en la ecuación original.
( )( )
( )( )
2 3
2 3 4
2 3 0 4 0
2 3 4 0
2 5 12 0
2 5 3 9 0
2 6 3 9
3 2 1 9
2
2
2
=
= = −
− = + =
− + =
+ − =
+ − − =
− + − =
+ − =
x
x x
x ó x
x x
x x
x x
x x x
x x
2) Halle las soluciones de 8 16 0 3 2
x − x + x = .
Solución:
Como la ecuación ya está igualada a cero solamente hay que factorizar e
igualar sus factores a cero y resolver en términos de x .
( 8 16) 0 2 x x − x + =
x(x −4)(x −4) = 0
x = 0 ó x −4 = 0
x = 4
Ejercicios:
Resolver cada ecuación por el método de factorización:
1) ( )( ) x +5 x −2 = 0
2) 3y 8y 9 2y 2 + − = 3) 9 4 0 2 x − =
4) 14 45 2 a − a = −
5) z( ) 2z −3 =14
6) 3 2 x −22x = 9x
Soluciones:
1) 2, –5
2) –3,1
3) 2/3, –2/3
4) 9, 5
5) 7/2, –2
6) 0, 11, –2
Objetivos
Esta lección presenta los conceptos y destrezas básicas que te permitirán:
- Factorizar expresiones cuadráticas de la forma x2 + bx + c.
- Factorizar expresiones cuadráticas de la forma ax2 + bx + c.
- Reconocer casos especiales que se pueden factorizar a simple vista en este tipo de factores:
- (ax + b)(ax - b)
- (ax + b)2
- (ax - b)2
Introducción.
Si observamos la expresión cuadrática x + 6 se puede ver fácilmente que no hay un factor común a los tres términos. Sin embargo, en la lección sobre Multiplicación de Expresiones Binomiales usamos la geometría del producto de los lados de un rectángulo para mostrar que 3 = x 2 + 5 x + 6
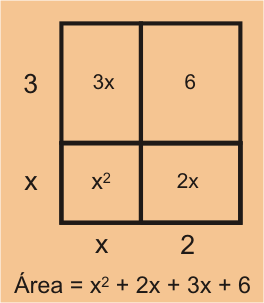
Por lo tanto (x + 2)(x + 3) es la factorización de + 5 x + 6 pero las técnicas de factorización son diferentes a las presentadas en la lección sobre Factorización de Expresiones Simples.
Esta lección se centra en los métodos de factorización de expresiones cuadráticas de la forma:
Esta lección se centra en los métodos de factorización de expresiones cuadráticas de la forma:
Coeficiente de x2 igual a 1.
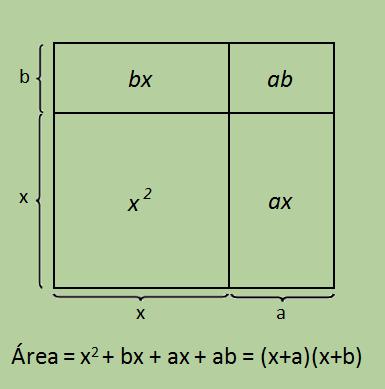
En la lección de Multiplicación de Expresiones Binomiales comenzamos con
Ahora queremos comenzar con y convertirlo en una expresión con dos factores de la forma
-
+ c x + d = x + a x + b -
a x + b = x 2 + a + b x + ab
De aquí podemos obtener el siguiente conjunto de pasos para factorizar expresiones de segundo grado con coeficiente de x2 igual a 1.
Ejemplo 1:
FactorizarSolución:
Buscamos a y b que satisfagan:-
+ 7 x + 12 = x + a x + b -
a x + b = x 2 + a + b x + ab
Paso 1: Buscar todos los pares (a, b) tal que ab = 12:
(12,1), (6,2), (4,3), (-12,-1), (-6,-2), (-4,-3)
Puesto que: |
Paso 2: Determinar si uno de estos pares cumple a + b = 7:
Así que a= 4, b= 3 cumple a + b = 7 y ab = 12. Por lo tanto: |
Paso 3: Verificar
|
Ejemplo 2:
FactorizarSolución:
Nota: Para mayor comodidad de nuestro método vamos a reescribir las diferencias como sumas de factores negativos, por lo que el problema se convierte en-
+ (-4) x + (-21) = x + a x + b -
a x + b = x 2 + a + b x + ab
Paso 1: Buscar todos los pares (a, b) tal que ab = -21:
(21,-1), (-21,1), (7,-3), (-7,3)
|
Paso 2: Determinar si uno de estos pares cumple que
a + b = -4: Así que a= -7, b= 3 cumple a + b = -4 y ab = -21. Por lo tanto: |
Paso 3: Verificar
|
Práctica 1.
Oprime el enlace a continuación para practicar la factorización de expresiones cuadráticas con coeficientes principales igual a 1.

Coeficiente de x2 diferente de 1.
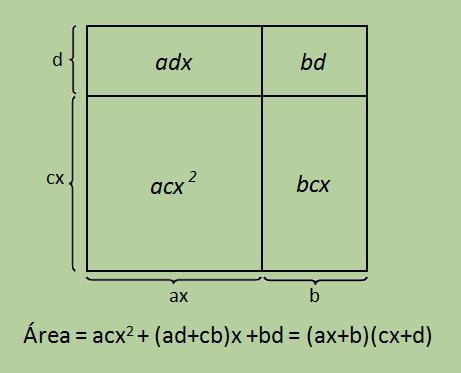
En la lección de Multiplicación de Expresiones Binomiales comenzamos con
Ahora queremos comenzar con y convertirlo en una expresión con dos factores de la forma
- =
c x + d -
c x + d ad + cb x + bd.
De aquí podemos obtener el siguiente conjunto de pasos para factorizar expresiones de segundo grado con coeficiente de x2 no igual a 1.
Ejemplo 1:
Factorizar:Solución:
Buscamos a, b, c y d asi que:- =
c x + d -
c x + d ad + cb x + bd.
Paso 1: Buscar todos los pares (a, c) tal que ac = 2:
(2,1), (1,2), (-2,-1), (-1,-2)
Como: a y c no son intercambiables y podemos repetir pares, tales como (2,1) y (1,2). | ||
Paso 2: Buscar todos los pares de (b, d) de tal manera que bd = 5:
Como: si intercambiamos a y c, no es necesario el intercambio b y d para crear una expresión equivalente. Como: no es necesario incluir los dos (x, y) y (-x,-y). Uno de ellos es suficiente. | ||
Paso 3: Sustituye todas las combinaciones de (a, c) y (b, d) para ver si uno satisface ad + cb = 11. No es necesario pero también sustituimos en
Ejemplo 2:
Factorizar:
Solución:
Buscamos a, b, c y d asi que:
Así, necesitamos a, b, c y d que satisfagan ac = 3, ad + cb = -5 y bd = -12
|
No hay comentarios:
Publicar un comentario