viernes, 14 de febrero de 2014
conclusion del tema ecuaciones cuadraticas por formula
se puede decir que este tema estuvo un poco facil ya que en la mayoria de los ejercicios me salia bien pero me confundia mucho en las comprobaciones pero lo entendi mucho mas gracias al blog
conclusion del tema regla de la suma
bueno casi no le entendi ya que es uno de los temas de probabilidad se me complico mucho ademas de que saque cero en el segundo bloque pero gracias al blog lo puedo repasar
conclusion del tema simetria central
el tema de simetria sentral lo vi algo facil ya que las dos figuras son separadas por un punto de union o una linea de simetria aunque tenia que estar iguales y casi no me daba me salia con medidas demas pero lo entendi
conclusion del tema homotecia
en este tema entendi que homotecia directa y homotecia inversa son algo parecidas con simetria central y simetria axial aunque cada una tiene su diferencia homotecia directa es cuando el punto h refleja a las dos figuras de un solo lado y homotecia inversa el punto h es el centro de homotecia y refleja las dos figuras en distintos lados
conclusion del tema teorema de pitagoras
en este tema yo entendi que se suman todos los catetos de un triangulo y la hipotenusa ademas de que se me hizo un poco dificil la parte de sacarlo por ejercicios aunque la mayoria me salio bien y le entendi aunque sea un poco
tabulacion y graficacion ejercicios
La forma mas sencilla de graficar una función cuadrática es tabulando. Esto es hacer un cuadro en donde se le dé varios valores a x (la variable independiente) para obtener y (la variable dependiente) y así con varios pares de coordenadas ubicar los puntos en un plano para trazar el gráfico de la función: por ejemplo:
Ahora vamos a tabular, asignándole valores a x, para ser reemplazados en la función y así obtener el valor de y, los cuales son los valores de f(x), y así obtener el par de coordenadas:

Al llevar estos pares de coordenadas al gráfico se obtiene el gráfico de la función:

La función cuadrática en su forma general y en su forma estándar permiten realizar de manera rápida el bosquejo de su gráfica:
- Forma general:
Esta es la expresión de su forma general, en donde a, b y c son los coeficientes de la ecuación.
Vale la pena analizar la ecuación anterior, pues de ella se obtiene información valiosa para efectuar el gráfico de la misma:
- Siempre la ecuación (en este caso la función) cuadrática se representa por medio de una parábola:

- Si el coeficiente a es positivo la función abre hacia arriba como en la gráfica. Si el coeficiente a es negativo, abre hacia abajo
- Cuando la función tiene únicamente el coeficiente a, la parábola no está desplazada como en la gráfica de arriba.
- Si la función cuadrática en su forma general, contiene solo los coeficientes a y c, la función está desplazada únicamente sobre el eje y. El desplazamiento hacia arriba ó hacia abajo está dado por el signo y el valor del coeficiente c. Veamos el siguiente gráfico:

- El valor de a = 1 dice que la parábola tiene una configuración normal. Para valores de a mayores a 1, la parábola está estirada (adelgazada) y para valores cercanos a 0, la parábola está más ancha.
- Si aparece el coeficiente b, la parábola tiene desplazamiento en ambos ejes, es decir su vértice está desplazado algunos valores tanto en el eje x como en el eje y.Por ejemplo:

Ahora, para realizar la gráfica se elabora una tabla de valores, asignándole valores a X (variable independiente) para obtener el valor de Y (variable dependiente). Una vez obtenidos los valores en la tabla, estos pares ordenados (x, y) se ubican en un plano cartesiano, para luego unir los puntos, obteniendo así la gráfica de la parábola.
- forma Estandar:
Aplicando la expresión para la función cuadrática en su forma estándar:  en donde a es el mismo coeficiente mencionado anteriormente, y los valores correspondientes a -h y k indican los desplazamientos en el eje x y yrespectivamente. Vemos el siguiente ejemplo:
en donde a es el mismo coeficiente mencionado anteriormente, y los valores correspondientes a -h y k indican los desplazamientos en el eje x y yrespectivamente. Vemos el siguiente ejemplo: , el coeficiente a= 2 (es decir la parábola está estirada), -h = 1 (al escribir -h cambiamos el signo del valor entre paréntesis) con lo cual el vértice está desplazado 1 posición en x a la derecha, y k =3, es decir el vértice se ubica 3 posiciones hacia arriba en el eje y.Veamos el gráfico:
, el coeficiente a= 2 (es decir la parábola está estirada), -h = 1 (al escribir -h cambiamos el signo del valor entre paréntesis) con lo cual el vértice está desplazado 1 posición en x a la derecha, y k =3, es decir el vértice se ubica 3 posiciones hacia arriba en el eje y.Veamos el gráfico: 

Lo primordial es pasar de la función cuadrática en su forma general a la función cuadrática en su forma estándar. Para hacerlo hay dos formas:
- Utilizando el método de factorización completando el cuadrado
- Aplicando la fórmula de máximo y mínimo de una función
jueves, 13 de febrero de 2014
formula general de las ecuaciones cuadraticas
Ecuación cuadrática/Fórmula general
Consideremos la ecuación general de segundo grado (ecuación cuadrática) que tiene la forma:  .
.
 .
.
Resolver esta ecuación implica encontrar el valor o los valores de  que cumplen con la expresión, si es que existen.
que cumplen con la expresión, si es que existen.
Cuando nos enfrentamos por primera vez en la vida a esta clase de problemas, la primera forma en la que se intenta dar una respuesta es probando con varios números hasta "atinarle" (ya sea por que nos sonría la buena fortuna, o por aproximación).
Algunos incluso prueban número tras número hasta hallar la solución (Método de la "Fuerza Bruta").
Después, conforme nos vamos enfrentando a mas problemas que involucran ecuaciones cuadráticas, descubrimos algunos métodos de solución. De los primeros que aprendemos (por simplicidad) están el "Método Gráfico" (Realizar la gráfica correspondiente a la ecuación cuadrática igualada a cero y observar en que abscisas la gráfica "toca o pasa" por el eje horizontal del plano cartesiano). Otro método que aprendemos es el "Método de Factorización" (Trabajar con la expresión cuadrática igualada a cero hasta dejarla expresada como multiplicación de otras dos expresiones algebraicas, y encontrar "por simple observación" los valores que hacen que estas últimas dos ecuaciones sean iguales a cero).
Las desventajas de estos métodos es que implican trabajo excesivo, y no se garantiza que se encuentre la solución de la ecuación (al menos una solución "Real").
El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".
 que cumplen con la expresión, si es que existen.
que cumplen con la expresión, si es que existen.Cuando nos enfrentamos por primera vez en la vida a esta clase de problemas, la primera forma en la que se intenta dar una respuesta es probando con varios números hasta "atinarle" (ya sea por que nos sonría la buena fortuna, o por aproximación).
Algunos incluso prueban número tras número hasta hallar la solución (Método de la "Fuerza Bruta").
Después, conforme nos vamos enfrentando a mas problemas que involucran ecuaciones cuadráticas, descubrimos algunos métodos de solución. De los primeros que aprendemos (por simplicidad) están el "Método Gráfico" (Realizar la gráfica correspondiente a la ecuación cuadrática igualada a cero y observar en que abscisas la gráfica "toca o pasa" por el eje horizontal del plano cartesiano). Otro método que aprendemos es el "Método de Factorización" (Trabajar con la expresión cuadrática igualada a cero hasta dejarla expresada como multiplicación de otras dos expresiones algebraicas, y encontrar "por simple observación" los valores que hacen que estas últimas dos ecuaciones sean iguales a cero).
Las desventajas de estos métodos es que implican trabajo excesivo, y no se garantiza que se encuentre la solución de la ecuación (al menos una solución "Real").
El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".

Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
- Si
 es menor que
es menor que  los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
- Si
 es mayor que
es mayor que  obtendremos dos valores distintos de X reales.
obtendremos dos valores distintos de X reales.
- Y si
 es igual que
es igual que  obtendremos dos valores de X reales e iguales.
obtendremos dos valores de X reales e iguales.
- Al término
 se le llama discriminante.
se le llama discriminante.
tomando en cuenta el orden de los términos: "a","b"y"c"=x²-6x+9
Introducción
Podemos resolver cualquier ecuación cuadrática completando el cuadrado — convirtiendo un polinomio en un trinomio cuadrado perfecto. Si completamos el cuadrado en la ecuación genérica  y luego resolvemos x, encontramos que
y luego resolvemos x, encontramos que 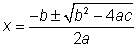 . Esta ecuación un poco extraña se conoce como fórmula cuadrática.
. Esta ecuación un poco extraña se conoce como fórmula cuadrática.
Esta fórmula es muy útil para resolver ecuaciones cuadráticas que son difíciles o imposibles de factorizar, y usarla puede ser más rápido que completar el cuadrado. La fórmula cuadrática puede ser usada para resolver cualquier ecuación cuadrática de la forma  .
.
Derivando la Fórmula Cuadrática
Vamos a completar el cuadrado en la ecuación general,  , para ver exactamente cómo se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:
, para ver exactamente cómo se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:
· Empezar con una ecuación de la forma 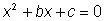 .
.
· Reescribir la ecuación de forma que 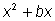 quede despejada.
quede despejada.
· Completar el cuadrado sumando 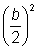 a ambos lados.
a ambos lados.
· Reescribir como el cuadrado de un binomio y resolver x.
¿Puedes completar el cuadrado en la ecuación cuadrática general  ? Inténtalo antes de continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación general
? Inténtalo antes de continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación general  , existe una complicación que consiste en que el coeficiente de
, existe una complicación que consiste en que el coeficiente de 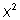 no es igual a 1. Puedes dividir la ecuación entre a, lo que hace que se compliquen algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al final, ¡obtendrás la fórmula cuadrática!
no es igual a 1. Puedes dividir la ecuación entre a, lo que hace que se compliquen algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al final, ¡obtendrás la fórmula cuadrática!
Ejemplo
| |||||
Problema
|
Completar el cuadrado de
| ||||
Dividir ambos lados de la ecuación entre a, para que el coeficiente de
| |||||
Reescribir de tal forma que el lado izquierdo tenga la forma
| |||||
Sumar
| |||||
Escribir el lado izquierdo como un binomio cuadrado
| |||||
Evaluar
| |||||
Escribir las fracciones del lado derecho usando un común denominador
| |||||
Sumar las fracciones de la derecha
| |||||
Sacar la raíz cuadrada de ambos lados. ¡Recuerda que debes conservar ambas raíces la positiva y la negativa!
| |||||
Restar
| |||||
El denominador bajo el radical es un cuadrado perfecto, entonces
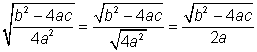 . . | |||||
Sumar las fracciones ya que tienen un común denominador
| |||||
Solución
| |||||
Y ahí la tenemos, la fórmula cuadrática.
La fórmula cuadrática funcionará para cualquier ecuación cuadrática, pero sólo si la ecuación está en su forma estándar,  . Para usarla, sigue los siguientes pasos:
. Para usarla, sigue los siguientes pasos:
· Primero transforma la ecuación a la forma estándar
· Identifica los coeficientes, a, b, y c. Ten cuidado de incluir los signos negativos si los términos bx o c están siendo restados.
· Sustituye los valores de los coeficientes en la fórmula cuadrática
· Simplifica lo más posible.
· Usa el ± enfrente del radical para separar la solución en dos valores: uno en el que la raíz cuadrada se suma, y el otro donde la raíz cuadrada se resta.
· Simplificar ambos valores para obtener las posibles soluciones.
Son bastantes pasos. Vamos a intentarlo:
Ejemplo
| ||||
Problema
|
Usar la fórmula cuadrática para resolver la ecuación
| |||
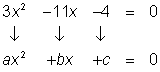 |
a = 3, b = -11, c = -4
Nota que la resta de signos significa que los coeficientes b y c son negativos
| |||
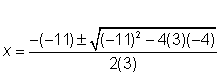 |
Sustituir los valores en la fórmula cuadrática
| |||
Simplificar, teniendo cuidado con los signos
| ||||
Simplificar más
| ||||
Simplificar el radical:
| ||||
o
|
Separar y simplificar para encontrar las soluciones de la ecuación cuadrática. Nota que en una, 13 es sumado y en la otra, 13 es restado
| |||
Solución
|
x = 4 o
| |||
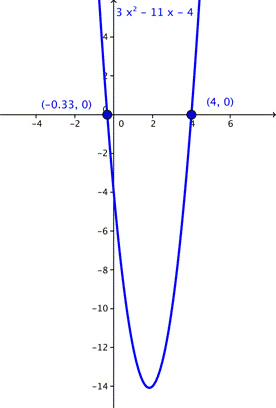
La solución para la ecuación cuadrática nos da las coordenadas en x de las intersecciones en x, o las raíces de una ecuación cuadrática. Las raíces de la ecuación cuadrática son los valores donde la parábola cruza el eje x. Podemos comprobar esto observando la gráfica de la función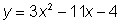 y ver que las raíces son (4, 0) y (
y ver que las raíces son (4, 0) y (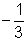 , 0).
, 0).
El ejemplo anterior muestra una ecuación cuadrática con dos soluciones. A continuación tenemos un ejemplo con una solución. Compara los radicales simplificados de los dos ejemplos:
Ejemplo
| |||||
Problema
|
Usar la fórmula cuadrática para resolver la ecuación
| ||||
Restar 6x de cada lado y sumar 16 a ambos lados para transformar la ecuación a su forma
| |||||
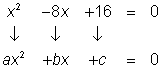 |
Identificar los coeficientes a, b, y c. x2= 1x2, entonces a = 1. Como 8x está siendo restado, b es negativo.
a = 1, b = -8, c = 16.
| ||||
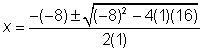 |
Aplicar la fórmula cuadrática
| ||||
Simplificar
| |||||
Como la raíz cuadrada de 0 es 0, y sumar o restar 0 dan el mismo resultado, existe sólo un valor posible
| |||||
Solución
|
x = 4
| ||||
Esta ecuación cuadrática sólo tiene una solución, por lo que la gráfica de la función 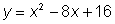 tocará el eje x una vez. Tiene una sola raíz.
tocará el eje x una vez. Tiene una sola raíz.

Algo que debemos notar — la ecuación cuadrática 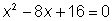 puede ser factorizada como
puede ser factorizada como 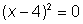 . Entonces, a pesar de que la fórmula cuadrática nos dio la solución, hubiera sido más fácil factorizarla. Vale la pena revisar si la ecuación cuadrática puede ser fácilmente factorizada antes de aplicar la fórmula cuadrática.
. Entonces, a pesar de que la fórmula cuadrática nos dio la solución, hubiera sido más fácil factorizarla. Vale la pena revisar si la ecuación cuadrática puede ser fácilmente factorizada antes de aplicar la fórmula cuadrática.
Usar la fórmula cuadrática para resolver la ecuación
A) x = 2
B) x =11, x = -9
C)
D)
|
El Discriminante
Una ecuación cuadrática puede tener dos raíces, una raíz, o ninguna raíz. En la fórmula cuadrática, la expresión bajo el símbolo radical determina cuántas soluciónes tendrá la fórmula. Esta expresión , 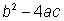 , se llama el discriminante de la ecuación
, se llama el discriminante de la ecuación  .
.
Pensemos en cómo 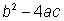 afectará la evaluación de
afectará la evaluación de 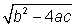 , y como nos ayuda a determinar el conjunto solución.
, y como nos ayuda a determinar el conjunto solución.
· Si 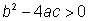 , entonces el número debajo del radical será un valor positivo. Siempre podemos calcular la raíz cuadrada de un número positivo, entonces al evaluar la fórmula cuadrática resultarán dos soluciones (una sumando la raíz cuadrada positiva, y la otra restándola).
, entonces el número debajo del radical será un valor positivo. Siempre podemos calcular la raíz cuadrada de un número positivo, entonces al evaluar la fórmula cuadrática resultarán dos soluciones (una sumando la raíz cuadrada positiva, y la otra restándola).
· Si 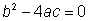 , entonces estaremos calculando la raíz cuadrada de 0, y el término "±" se deshace de la evaluación de la fórmula cuadrática. (Sumar cero y restar cero nos da el mismo resultado.) Esto será una solución.
, entonces estaremos calculando la raíz cuadrada de 0, y el término "±" se deshace de la evaluación de la fórmula cuadrática. (Sumar cero y restar cero nos da el mismo resultado.) Esto será una solución.
· Si 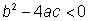 , entonces el número debajo del radical será un valor negativo. Como no podemos calcular la raíz cuadrada de un número negativo (por lo menos no usando el sistema de números reales), no podemos seguir evaluando la fórmula. Entonces no habrá soluciones.
, entonces el número debajo del radical será un valor negativo. Como no podemos calcular la raíz cuadrada de un número negativo (por lo menos no usando el sistema de números reales), no podemos seguir evaluando la fórmula. Entonces no habrá soluciones.
Ejemplo
| ||||
Problema
|
Usar el discriminante para determinar si la ecuación cuadrática
| |||
Evaluar
a = 1, b = -4, y c = 10.
| ||||
El resultado es un número negativo. El discriminante es negativo, por lo que la ecuación cuadrática no tiene solución.
| ||||
Solución
|
no hay solución
| |||
Supón que una ecuación cuadrática tiene un discriminante igual a cero. ¿Cuál de las siguientes declaraciones es siempre verdadera?
A) La ecuación tiene dos soluciones y la gráfica de la parábola abrirá hacia arriba.
B) La ecuación tiene una solución y la gráfica de la parábola abrirá hacia abajo.
C) La ecuación tiene una solución y no podemos decir nada sobre la dirección de la parábola.
D) La ecuación no tiene solución y no podemos decir nada sobre la dirección de la parábola.
|
Sumario
La fórmula cuadrática, 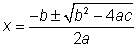 , se obtiene al completar el cuadrado de la ecuación cuadrática
, se obtiene al completar el cuadrado de la ecuación cuadrática  . La fórmula puede ser usada para encontrar la solución de una ecuación cuadrática e identificar cualquier raíz posible, o las intersecciones en x, de la función.
. La fórmula puede ser usada para encontrar la solución de una ecuación cuadrática e identificar cualquier raíz posible, o las intersecciones en x, de la función.
El discriminante de una fórmula cuadrática es la cantidad debajo del radical , 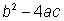 . Determina cuántas soluciones existen para la ecuación cuadrática. Si el discriminante es positivo, hay dos raíces. Si es cero, existe una raíz. Si el discriminante es negativo, no existen raíces.
. Determina cuántas soluciones existen para la ecuación cuadrática. Si el discriminante es positivo, hay dos raíces. Si es cero, existe una raíz. Si el discriminante es negativo, no existen raíces.
Suscribirse a:
Entradas (Atom)




